Article écrit par BACHOTET Sébastien
Article disponible également sur le site obligement.fr
La passion du numérique
Dans cet article, nous allons voir comment créer un processeur sur 4 bits, processeur très basique avec seulement quelques instructions.
Processeur 4 bits de type Harvard avec deux mémoires (instructions et données) et :
- les données sont des entiers en C2 (complément à deux « valeurs positives et négatives » soit des bits signés) sur 4 bits et les bus d’adresse sont aussi sur 4 bits.
- le processeur dispose de quatre registres (4 bits) programmables nommés R0, R1, R2 et R3 utilisés comme des variables. Le nom donné aux quatre registres est « Registre File ».
Le nom de la structure « Harvard » vient du nom de l’université Harvard où cette architecture a été mise en pratique pour la première fois avec le Mark I en 1944. Avec deux bus distincts, l’architecture dite de Harvard permet de transférer simultanément les données et les instructions à exécuter. Ainsi, l’unité de traitement aura accès simultanément à l’instruction et aux données associées.
Pour rappel, la famille des processeurs Motorola 68k et PowerPC sont de type Von Neumann. Il a une seule mémoire pour le programme et les données. De leur côté, les processeurs Intel IA32 (x86) et 64 bits, ainsi que les ARM, sont de type Harvard.
Il existe également des CPU (processeurs) qui utilisent les structures matérielles Harvard et Von Neumann dans leurs implémentations, dont notamment les DSP (Digital Signal Processor – processeur de signal numérique) utilisés par exemple pour le traitement du son numérique.
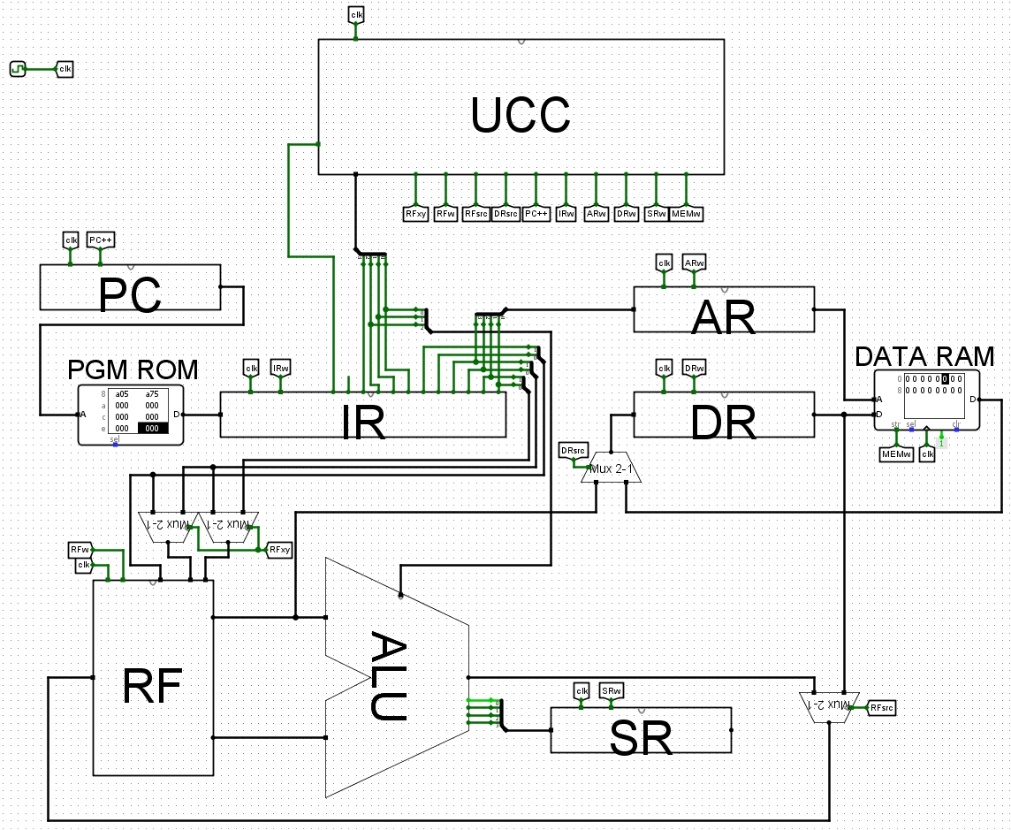
Schéma de principe du processeur 4 bits décrit dans cet article
Cet article est constitué de trois parties : la première concerne les circuits logiques et combinatoires, la deuxième sera consacrée à la partie séquentielle d’un circuit et, pour finir en partie 3, la réalisation du processeur 4 bits.
Cet article est inspiré par le livre Digital Design And Computer Architecture, 2e édition, écrit par David Money Harris et Sarah L. Harris.
Première partie : circuits logiques et combinatoires
- 1. Introduction
- 2. Définition d’un circuit combinatoire
- 3. Portes logiques
- 4. Règles de construction d’un circuit combinatoire
- 5. Spécifications d’un circuit combinatoire
- 6. La valeur Z et son utilisation dans les bus
- 7. La conception par composition en cascade
- 8. La réalisation de l’additionneur sur 1 bit
- 9. Annexe (liste des composants TTL)
1. Introduction
1.1 Informatique
Le terme désigné par « Informatique » peut-être séparé en deux parties. La partie « hardware » correspond au matériel et la partie « software » concerne les logiciels ou programmes informatiques.
Dans cet article, nous abordons uniquement la partie matérielle, conçue avec l’électronique numérique. Nous ne traitons pas la partie programmation ou logiciels permettant de piloter le matériel. Nous laissons également de côté l’électronique analogique qui n’est pas utile pour la réalisation de ce processeur.
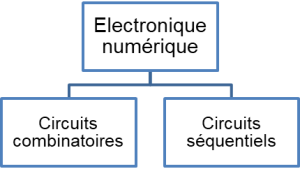
L’électronique numérique comprend : les circuits combinatoires (statiques ne possédant pas de mémoire) et les circuits séquentiels (dynamiques possédant une mémoire).
Pour rappel, l’électronique numérique est basée sur la valeur logique 0 et 1. Par exemple, avec une tension de 5 volts, le 1 binaire est égal à 5 volts et le 0 binaire est égal à 0 volt.
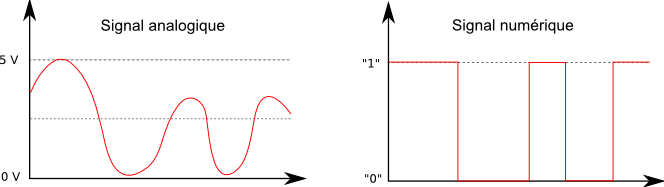
1.2 Représentation d’un signal analogique et d’un signal numérique
On peut remarquer que la courbe du signal numérique est une forme de type signal carré et que le signal analogique est une forme sinusoïdale (le courant de votre prise de courant chez vous en 230 volts est un signal sinusoïdal produit par des générateurs d’électricité, un alternateur par exemple). La forme sinusoïdale ne permet pas de connaître avec précision l’état de l’information que nous voulons utiliser (la position haut ou bas de la courbe n’est jamais constante). Dans un signal de forme carrée, nous avons un état haut (bit à 1) et un état bas (bit à 0) constant.
Principe du passage de l’analogique au numérique
Tension à 5 volts : le bit est à 1
Tension à 0 volt : le bit est à 0
En exemple, vous allumez la lumière d’une pièce en appuyant sur un interrupteur, cela correspond à un état 1. Quand vous appuyez sur l’interrupteur une nouvelle fois pour ouvrir le circuit, la lumière s’éteint, c’est l’état 0.
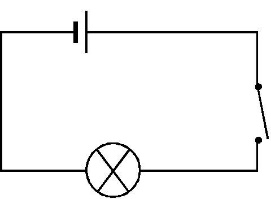
L’interrupteur est ouvert, le courant ne circule pas, la lampe ne fonctionne pas, c’est l’état 0
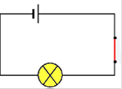
L’interrupteur est fermé, le courant circule dans les conducteurs, la lampe est allumée, c’est l’état 1
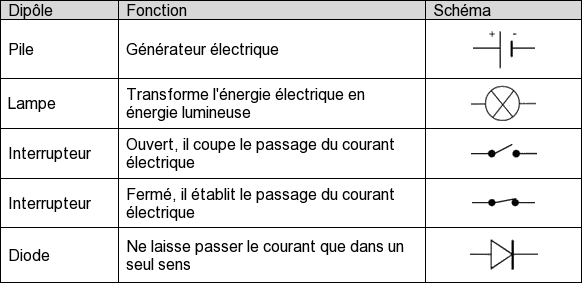
Symboles des dipôles
1.3 Définition du binaire
Le binaire est composé de l’expression 1 ou 0 afin de décrire une information.
Un encodage sur 4 bits correspond à quatre informations (0 et 1) soit : 0000, 0001 ou 0010, etc. produit par exemple avec quatre interrupteurs. Sur 8 bits « 0000 0000 », cela correspond à huit interrupteurs pouvant avoir soit la position ouvert (0) ou fermé (1). Une information codée sur 4 bits s’appelle un « nibble » soit un demi octet et une information sur 8 bits représente un « octet ». C’est une valeur d’occupation pour l’information binaire.
2. Définition d’un circuit combinatoire
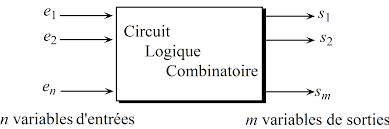
Un circuit combinatoire (C.C.) est un composant (forme carrée en électronique) qui comporte des entrées et une ou plusieurs sorties. On les appelle « ASI » ou « chipset » en anglais. Ils réalisent des traitements binaires entre les entrées et les sorties.
Les circuits combinatoires possèdent « n » entrées et « m » sorties binaires (uniquement 1 et 0 en entrée et en sortie). Un circuit combinatoire est à base soit de TV et/ou de FB (cela correspond à sa spécification/description) : soit le circuit est à base de TV (en utilisant la table de vérité) ou FB qui est la fonction algébrique booléenne.
E = entrée (donnée brute)
S = sortie (résultat)
Dans cet article, nous utilisons ses deux outils mathématiques permettant de réaliser un circuit combinatoire. On peut également dire que la spécification est la description d’une technologie contrairement à l’implémentation qui concerne la réalisation.
3. Les portes logiques
Les portes logiques sont construites par de l’électronique analogique. Cela comprend, par exemple, les résistances, les diodes, les condensateurs, etc. qui sont interconnectés par des liaisons électriques. Nous allons voir les sept portes logiques les plus utilisées.
Important : une porte logique est un composant élémentaire de base, il est indivisible, il ne peut pas être subdivisé. C’est un élément basique et physique. Ils sont assemblés en composition pour former les circuits numériques. Ils représentent une opération élémentaire de la logique booléenne (ET, OU, NON, etc.).

Représentation d’un élément physique
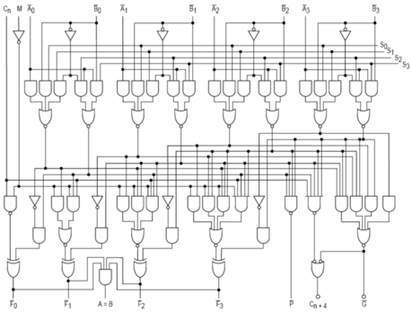
Représentation du circuit interne « UAL » ou « ALU » (Unité Agrimétrique Logique) à partir de portes logiques.
Composant type 74181 utilisé dans les années 1980.
Une opération logique utilise des conditions. Exemple : il faut avoir 18 ans ou plus pour conduire un véhicule et il faut un permis de conduire. Nous avons donc deux conditions pour conduire un véhicule (l’âge et le permis). Soit la condition logique « ET » (« AND » en anglais).
3.1 Portes logiques
3.1.1 La porte logique « AND » (ET)

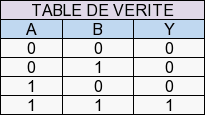
C’est le « ET » logique : Y=A-B. Exemple : A=0 et B=0 alors Y=0 ; A=1 et B=1 alors Y=1.
La table de vérité permet de savoir l’état de sortie (Y) selon les entrées A et B. Ici, la porte « AND » a besoin de A et B à l’état logique 1 pour que la sortie soit aussi à l’état logique 1. Si A et B ne sont pas à 1, alors Y=0
3.1.2 La porte logique « OR » (OU)

C’est le « OU » logique : Y=A+B.
3.1.3 La porte logique « NOT » (NON)
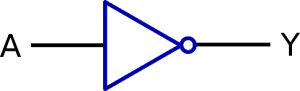
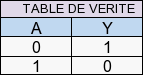
C’est le « NON » logique : Y=Ā. Cette porte ne comporte qu’une seule entrée.
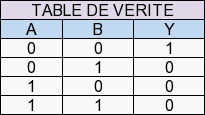
3.1.4 La porte logique « NAND » (NON-ET)

C’est l’inverse de la porte « AND »
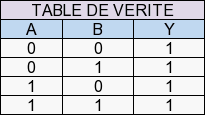
3.1.5 La porte logique « NOR » (NON-OU)
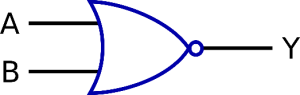
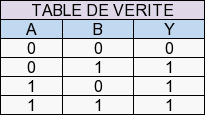
C’est le NON-OU logique : Y=A+B.
C’est l’inverse de la porte « OR » (OU).
3.1.6 La porte logique « XOR » (OU exclusif)

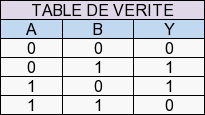
C’est le « OU exclusif » logique : Y=A⊕B. C’est un « OR » (OU) particulier. Il exclut A et B quand ils valent 1, soit en sortie Y=0.
Par exemple, en voiture, quand j’arrive à une intersection avec seulement une direction à gauche ou à droite, c’est une condition exclusive A=à droite, B=à gauche, la sortie Y ne peux pas avoir A et B ensemble (il faut choisir entre A ou B exclusivement).
3.1.7 La porte logique « XNOR » (NON-OU exclusif)

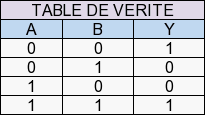
C’est le NON-OU exclusif logique : Y=A⊕B=A⊗B.
C’est l’inverse de la porte « XOR ».
3.2 Autres composants
3.2.1 Le « buffer » (tampon)


Il ne fait aucune opération logique, il est utilisé pour réduire la vitesse d’un signal dans certaines conditions. Comme pour la synchronisation de signaux, par exemple. Y=A.
3.2.2 Le « tri state buffer » (le tampon à trois états)
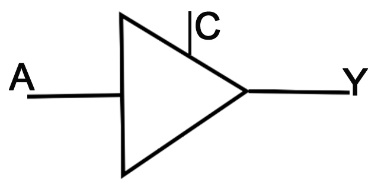
Il ne produit pas de réponse logique, mais va produire un nouveau signal. C’est un tampon à trois états, ça permet d’utiliser le signal logique Z (valeur flottante). Nous verrons son utilisation plus en bas dans l’article
3.3 Les caractéristiques des portes logiques
3.3.1 Le fan-out
Le « fan-out » correspond au nombre de portes logiques combinées à la sortie d’une porte logique. Par exemple, fan-out=3, cette indication montre que la porte logique en sortie ne peut être combinée avec un maximum de trois autres portes logiques. S’il y a quatre portes logiques en sortie de la première, le circuit combinatoire devient instable et son fonctionnement n’est plus garanti. On retrouve cette information dans la fiche technique du fabricant du composant.
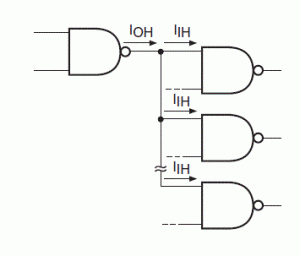
Représentation avec trois portes NAN connectées en sortie de la première porte logique NA
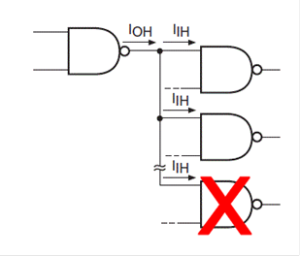
Si le fan-out est égal à 2, alors il ne faut pas trois portes logiques en sortie.
3.3.2 Le Fan-in
Le fan-in correspond au nombre d’entrées sur une porte logique. La porte logique « AND » comprend une entrée A et B. Il peut être nécessaire d’avoir plusieurs entrées comme A, B et C par exemple. On l’appellera alors « AND3 ».
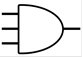
Représentation de la porte logique « AND3 fan-in=3 »
4. Règles de construction d’un circuit combinatoire
Un circuit combinatoire est un circuit qui regroupe plusieurs portes logiques afin d’obtenir un traitement automatique d’une information. Il faut définir formellement et mathématiquement le fonctionnement du circuit combinatoire. Un circuit combinatoire est décrit formellement comme un graphe constitué d’éléments et de liens orientés.
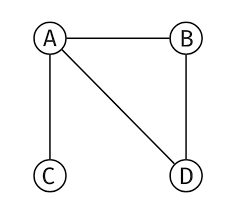
Par exemple, A est une ville et B une autre ville, elles sont reliées par une seule route (lien). B et C ne sont pas reliées directement. Pour rejoindre C en partant de B, il faut passer par A. Les graphes permettent de définir mathématiquement le meilleur chemin pour aller d’un point à un autre.
5. Les spécifications d’un circuit combinatoire
5.1 Les deux premières règles
- L’élément (C.C. ou P.L.) (circuit combinatoire ou porte logique).
- Le lien = fil électrique transportant 0/1 (0 volt ou 5 volts).
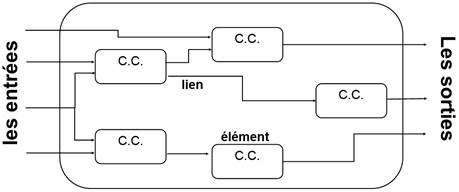
Représentation d’un circuit construit avec d’autres circuits combinatoires
Dans cette représentation, nous observons quatre entrées et trois sorties. Les entrées arrivent sur d’autres circuits combinatoires et produisent une réponse en sortie soit à travers des liens intermédiaires (entre deux circuits combinatoires ou éléments) ou des liens de sorties directement sur l’extérieur.
Un circuit combinatoire peut comporter d’autres circuits combinatoires à l’intérieur. L’élément le plus petit dans un circuit combinatoire est la porte logique.
Pour la conception d’un circuit combinatoire complexe, il est nécessaire de le subdiviser en petite partie (en petit circuit) qui seront ensuite assemblés pour complexifier le circuit.
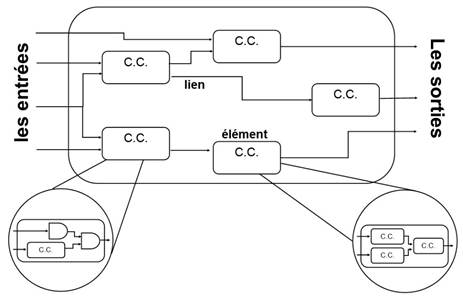
Représentation d’un circuit combinatoire avec l’élément le plus petit, la porte logique « en bas à gauche
5.2 La troisième règle est la combinaison
Pour chaque combinaison d’entrée « n », doit correspondre une unique combinaison de sortie « m ».

Ici, nous avons quatre entrées « n » combinées (E1, E2, E3 et E4) qui correspondent par exemple à « 0100 » et quatre sorties « m » combinées (S1, S2, S3 et S4) en résultat « 0001 ». Le terme de « combinaison » correspond au terme de probabilité.
Exemple : avec trois variables non définies qui utilisent la valeur booléenne (soit 1 ou 0), combien de combinaison est-il possible de réaliser ?
Les combinaisons possibles :
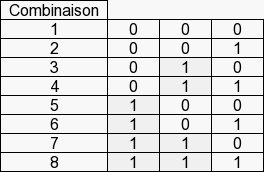
Le résultat est 8 : trois valeurs avec deux variables possibles (0 et 1). Avec 3 bits, il y a huit combinaisons possibles. Il est possible de définir quelles seront les résultats des sorties selon les entrées. Avec les portes logiques, il est possible de construire une logique définie.
Exemple : en entrée « 110 » ; en sortie, il est alors possible de définir « 010 ».
Attention à ne pas confondre les circuits combinatoires avec les circuits séquentiels. Nous sommes sur un circuit combinatoire qui est statique. Il produit toujours la même valeur en sortie selon la valeur d’entrée. Un circuit séquentiel produit un résultat en sortie qui change avec les mêmes données en entrée, il est dynamique.
5.3 Quatrième règle, l’entrée d’un élément qui ne peut recevoir qu’une unique sortie précédente (contorsion ou conflit)
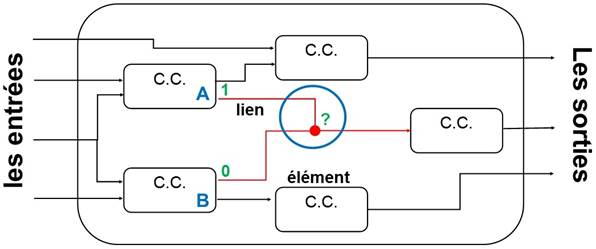
Le circuit combinatoire A (C.C. A) et le B (C.C. B) en sortie rentrent dans la même entrée du circuit combinatoire à gauche (C.C.). Nous sommes en présence d’une contorsion. Il n’est pas possible pour l’entrée du circuit combinatoire de gauche (C.C.) de connaître l’état de la valeur binaire à sa porte.
5.4 Dernière règle, le chemin d’un signal ne peut pas traverser un élément plus d’une fois (boucle/cycle)
Les boucles et les cycles sont interdits à l’intérieur d’un circuit combinatoire.
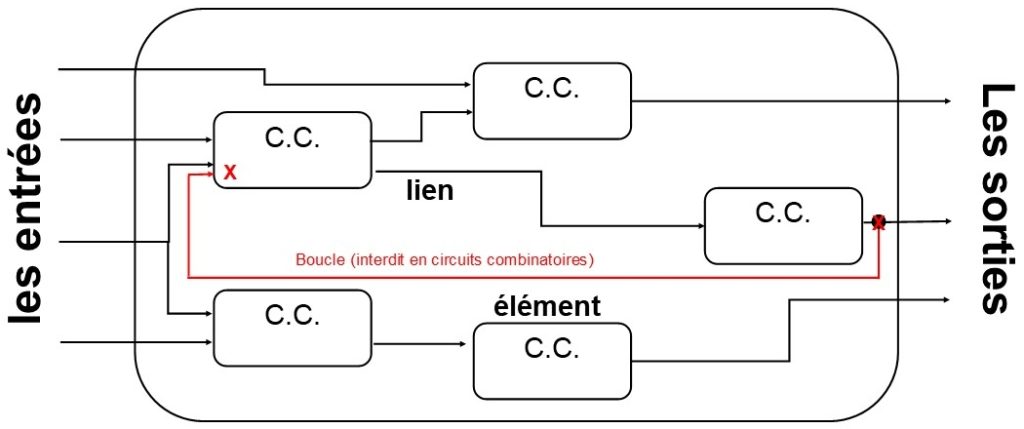
Il n’est pas possible de transmettre le résultat (fil en rouge) dans le premier circuit combinatoire (C.C.) de gauche issue de la sortie du dernier circuit combinatoire (C.C.) de droite. A l’inverse, dans les circuits séquentiels, la boucle est obligatoire, les sorties reviennent dans les entrées.
6. La valeur Z et son utilisation dans les bus
La valeur Z ou l’état Z est le troisième état logique en comptant l’état 0 et l’état 1. La valeur Z est une valeur flottante ou à haute impédance (résistance).
6.1 Pourquoi la valeur Z
L’état binaire 1 est la résultante de la tension portée à 5 volts sur un fil. Il en va de même pour l’état 0 qui est la résultante de la tension à 0 volt. La tension est la différence de potentielle entre deux points. Nous pouvons également comparer ça à un château d’eau et à la pression au robinet qui dépendra de la hauteur du château d’eau. Si nous prenons une pile de 1,5 volt, nous avons une borne « + » (positive) et une bonne « – » (négative).
Dans le schéma à droite, la lampe est alimentée par une pile avec un dispositif de commande qui est l’interrupteur. On peut considérer que la lampe qui est allumée est à l’état 1. En ouvrant l’interrupteur, le courant ne circule plus, la lampe est éteinte.
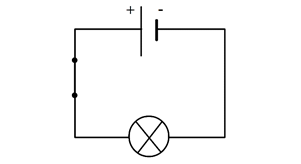
Ici, la lampe est éteinte parce que nous avons ouvert l’interrupteur alors l’état logique est 0.
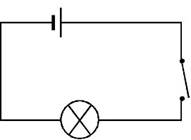
Cependant, dans cette configuration, nous ne sommes pas certains que le fil qui part de l’interrupteur à la lampe soit vraiment à 0 volt. La raison à cette cause est l’environnement autour du fil. Un fil est un conducteur et comme tous conducteurs, il est sensible au champ électromagnétique. De ce fait, il peut y avoir des tensions parasites sur le fil (conducteur) et ne pas avoir un vrai 0 volt absolu.
Un fil parcouru par un signal avec une valeur Z (ou X dans les logiciels de simulation) signifie que le fil n’est pas branché, ni à 0 ni à 1, on peut dire qu’il est dans le vide. Il n’est raccordé à rien (pas au « + » ni au « – » de la pile ou de l’alimentation).
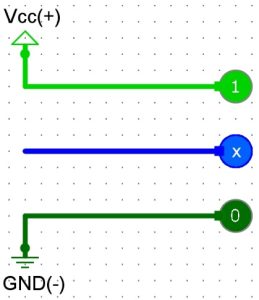
Dans ce schéma, Vcc est le « + » de la pile et GND est le « -« . L’état logique de la lampe sur Vcc est le 1. L’état logique de la lampe sur GND est le 0. L’état logique de la lampe du milieu est Z (notre interrupteur ouvert).
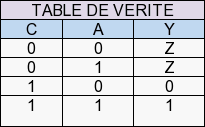
6.2 Le tampon à trois états (« tristate buffer »)
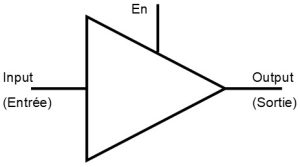
Table de vérité

Le tampon à trois états ne change pas l’état du signal d’entrée (input) à la sortie (output). Cependant, il possède une entrée de commande (En). Il est nécessaire de préciser que le rôle de la valeur Z est de détourner la règle 4 de la définition des circuits combinatoires. C’est-à-dire que l’entrée d’un élément ne peut recevoir d’une unique sortie précédente, sinon il y a risque de contorsion ou conflit. Il va donc être possible d’avoir plusieurs sorties sur le même fil, on appelle ça un bus, il est utilisé pour transporter de l’information.
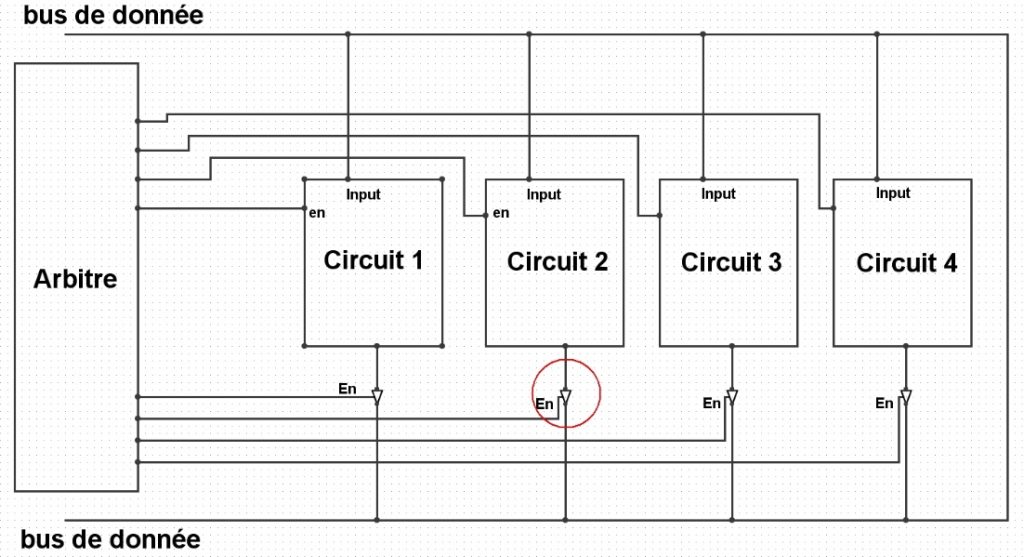
Représentation de plusieurs circuits communiquant à travers un fil (bus) commandée par un arbitre
Dans le schéma ci-dessus, un fil (bus) fait le tour des circuits et les extrémités à gauche ne sont raccordées à rien. On remarque que le fil est utilisé pour les quatre circuits en entrée et en sortie également. Si le circuit 1 et 3 sortent la valeur 0 et les circuits 2 et 4 sortent la valeur 1, nous sommes en conflit sur le bus à cause des quatre valeurs qui arrivent en même temps sur le même fil.
Pour les circuits 1, 3 et 4, les tampons à trois états (cercle rouge) vont empêcher que la valeur soit 1 ou 0 sur le bus en produisant la valeur Z (fil dans le vide). Il n’y aura que le circuit 2 qui enverra sa valeur 1 ou 0 sur le bus.
Les tampons à trois états sont commandés par l’arbitre de bus qui envoie sur l’entrée « En », la valeur 0 indiquant de passer à la valeur Z ou 1 afin de transmettre la valeur de sortie du circuit concerné (0 ou 1).
Ici, l’arbitre possède huit fils de commandes. L’information est envoyée à tous les circuits en même temps. Les quatre premiers fils d’en haut communiquent la commande 0 ou 1 aux circuits 1, 2, 3 et 4 et donnent l’autorisation de lire l’information provenant du bus (entrée « En » sur les circuits). Les quatre fils du bas commandent les tampons à trois états de chaque sortie des circuits.
Dans les années 1980, l’arbitre de bus était réalisé avec un simple décodeur. Dans les années 2000, il était implémenté dans les jeux de composants. Aujourd’hui, l’arbitre de bus est implémenté dans le processeur.
6.3 Les états 0-faible et 1-faible en relation avec le signal Z
Certains circuits ne tolèrent pas l’utilisation de Z dans leurs entrées et peuvent dysfonctionner. Ils n’acceptent pas de valeur flottante. La valeur Z doit être remplacée par un état 0 ou 1. La réalisation de circuit avec la valeur Z est une mauvaise façon de conception, les valeurs Z ne sont pas stables (ni 0 ni 1).
Pour éliminer le signal Z, il existe deux autres états : l’état 0-faible et l’état 1-faible. Ils sont utilisés pour remplacer le Z dans les bus vide, les bus sans 0 ni 1. Ils vont permettre de remplacer l’état Z sur un bus en 0-faible ou 1-faible. Les états « faible » sont des constantes fixes, ils ne peuvent pas changer, ils sont définis lors de la conception du circuit en ajoutant des résistances.
Dans le schéma ci-dessous, une entrée à l’état 0 sur le tampon à trois états (en haut) :
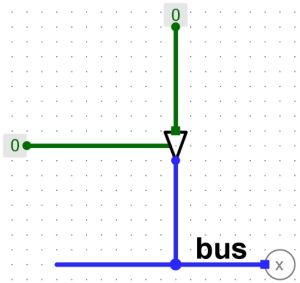
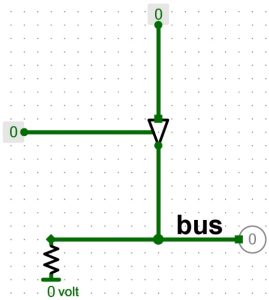
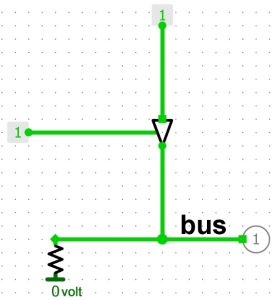
Le tampon à trois états reçoit l’information 0 lui indiquant de ne pas transmettre l’information de son entrée et de passer au signal Z (X dans le schéma). Une résistance « Pull down » est placée entre le 0 volt et le fil du bus. Cette méthode permet de supprimer le signal Z sur le bus et de placer la valeur 0-faible. Pour la valeur 1, on place la résistance « Pull up » avec le 5 volts.
En l’absence de la résistance (100 KΩ pour une tension de 5 volts), la valeur du bus serait Z (aléatoire, inconnu). Il serait possible de placer le fil directement sur le 0 volt, mais dans cette configuration, le bus à une valeur constante, ce qui produirait un conflit si la valeur 1 apparaît. Avec cette résistance qui produit un 0-faible sur le bus et si la valeur 1 se présente, cette valeur prend le dessus sur la valeur 0-faible.
7. La composition en cascade
La modularité est la manière de concevoir un circuit en le subdivisant en circuits plus petits. La composition en cascade est similaire à la modularité, à condition que les petits soient du même type que le plus grand. C’est applicable sur certains circuits ce qui les rend très flexibles.
7.1 Exemple 1 : construction d’un multiplexeur 4-1 (Mux 4-1) à partir de deux Mux 2-1
Pour rappel, un Mux est un aiguilleur de signal, avec deux entrées (1 et 2) et une seule sortie. Le Mux 2-1 sort l’information de l’entrée 1 ou 2 sur la sortie, en fonction de son entrée de commande (0 ou 1).
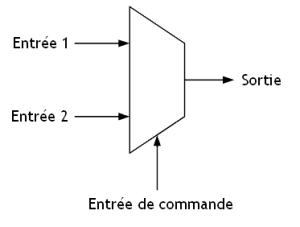
Représentation d’un multiplexeur Mux 2-1
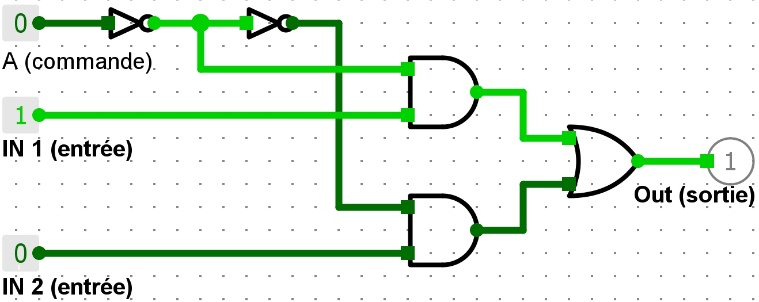
L’intérieur du Mux 2-1 avec les portes logiques
En entrée de commande :
0 = la valeur de l’entrée 1 (IN 1) en sortie (Out).
1 = la valeur de l’entrée 2 (IN 2) en sortie (Out).
Assemblage Mux 4-1 avec trois Mux 2-1
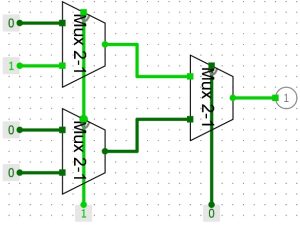
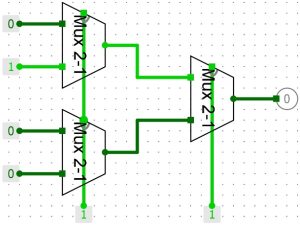
Assemblage de trois Mux 2-1 pour construire un Mux 4-1
L’entrée de commande est commune aux deux premiers des Mux de gauche. La deuxième entrée de commande est unique au Mux de droite. Nous avons donc 2 bits pour les entrées de commande avec quatre possibilités (00, 01,10 et 11).
7.2 Exemple 2 : construction d’un additionneur 4 bits
En binaire, nous disposons de la valeur 0 et 1 pour l’ensemble des opérations. Sur 4 bits, nous disposons de :

Sur 4 bits en décimal, nous pouvons compter de 0 à 15 :
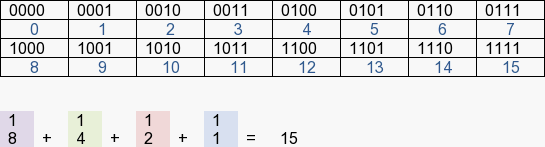
En binaire/décimal :
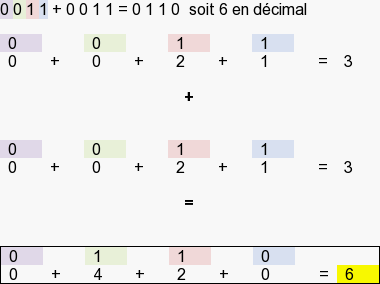
Ou avec la table de calcul :
- 1+1=2 soit 10 en binaire. Je pose 0 et je retiens 1
- 1+1=10+(la retenue)1=11. Je pose 1 et je retiens 1
- 0+0=0+(la retenue)1=1. Je pose 1
- 0+0=0. Je pose 0
- Résultat = 0110
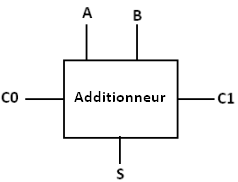
Illustration d’un additionneur

Les portes logiques d’un additionneur complet sur 1 bit
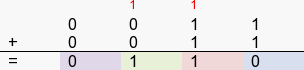
L’entrée A et B correspondent à l’addition de la première colonne de droite. Le résultat (S) est 10 en binaire (soit 2 en décimal).
Sur la sortie S, nous trouverons l’état = 0. Sur la sortie C1 ou (Cout), la retenue qui fait = 1.

L’entrée C0 (Cin) n’est pas utilisée pour la première opération (pas de retenue).
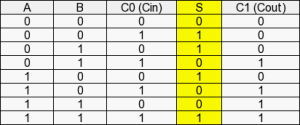
Vérifions l’additionneur avec la table de vérité :
Pour pouvoir calculer sur un ensemble de 4 bits, il faut rajouter trois additionneurs au premier.
La sortie C1 (la retenue) du premier additionneur est raccordée à l’entrée C0 du second additionneur et ainsi de suite.
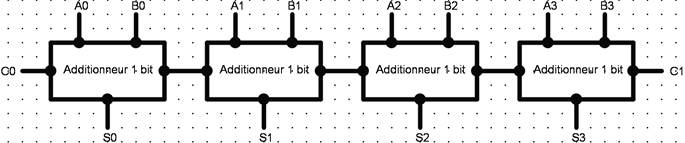
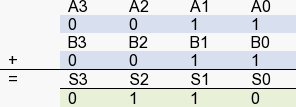
Le résultat est sur 4 bits (S0, S1, S2 et S3), soit dans notre exemple : 0110=6 en décimal.
Essayons : 1001+1001 (en décimal : 9+9=18)

Dans ce cas de figure, l’opération (18 en décimal) tient sur 5 bits. Notre additionneur ne fait que 4 bits en sortie, nous avons ici en sortie C1 un « dont’t care », un débordement représenté par l’état 1.
Concevoir l’additionneur avec des portes logiques en utilisant les fonctions canoniques disjonctives
Calcul de la fonction S. Calcul de la fonction C1 (Cout).
Avec la table de vérité, nous recherchons dans la colonne S et C1 tous les états à 1 :
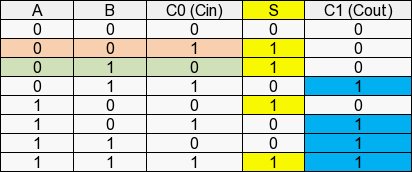
On peut dire que :
- S (A,B,C0)
- C1 (A,B,C0)
Dans la formule ci-dessous, nous allons chercher pour S et C1 tous les états à 1 et placer une barre au-dessus de A, B ou C0 (c’est-à-dire Ā, B̅ et C̅0̅) si la valeur est à 0 pour chaque ligne du tableau.
Nous avons quatre items avec 1 à S et quatre items avec 1 à C1.
- S (A,B,C0) = Ā.B̅.C0+Ā.B.C̄0̄+A.B̅.C̄0̄+A.B.C0
- C1 (A,B,C0) = Ā.B.C0+A.B̅.C0+A.B.C̄0̄+A.B.C0
Le résultat de l’équation est long, ce qui entraîne beaucoup de portes logiques. Il faut réduire au maximum l’équation pour limiter le nombre de portes logiques. Les avantages de la réduction sont nombreux, comme le coût réduit, moins de place occupée sur le circuit et l’augmentation de la vitesse d’exécution des opérations. Il faut prendre en compte l’effet de la propagation de la retenue à chaque additionneur. La retenue doit passer du premier additionneur au suivant, etc. Le résultat final ne sera juste, que lors la propagation de la retenue sera terminée dans le circuit.
La réduction en utilisant la table de Carlo
Nous prenons la sortie C1 soit :
- C1 (A,B,C0) = Ā.B.C0+A.B̅.C0+A.B.C̄0̄+A.B.C0
Pour rappel, A=1, Ā=0, B=1, B̅=0, C0=1, C̄0̄=0.
Nous allons pour chaque item placer « 1 » dans la table de Carlo.
Pour le premier = Ā.B.C0
Ā-B = 01-C0 = 1
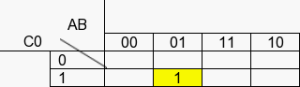
Pour le deuxième item = A.B̅.C0
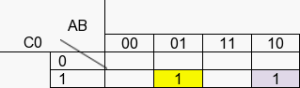
Pour le troisième item = A.B.C̄0̄
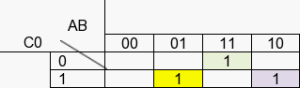
Le dernier item = A.B.C0
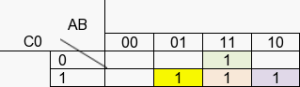
Les cases vides correspondent à 0.
Dans cette dernière table, nous allons faire des ensembles par paire pour les valeurs de 1.
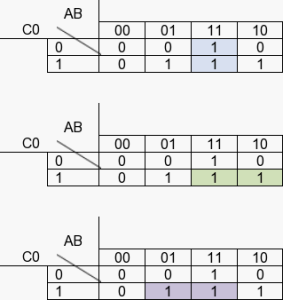
Nous avons réduit à trois items, soit : A.B.C0 A.B.C0 A.B.C0
Nous allons encore réduire en éliminant les valeurs qui changent pour chaque item.
Item 1 : A.B.C0
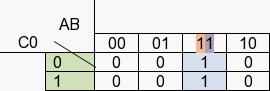
- A=1B=1 : la valeur est identique à 1 dans le tableau.
- C0=0 ou 1, alors que dans le tableau, la valeur est 1, la valeur change, C0 est supprimée.
- Résultat : C1(A,B,C0) = A.B
Item 2 : A.B.C0
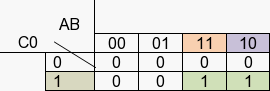
- A=11 : pas de changement.
- B=10 : il n’est pas identique à 1 et 1 du tableau, B est supprimée.
- C0=1 : il ne change pas.
- Résultat : C1(A,B,C0) = A.C0
Item 3 : A-B-C0
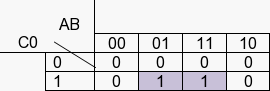
- Résultat : C1(A,B,C0)=B.C0
Soit la réduction suivante pour la sortie C1 :
- C1(A,B,C0)=A.B+A.C0+B.C0
Maintenant, nous allons faire la même chose pour la sortie S :
- S(A,B,C0)=Ā.B̅.C0+Ā.B.C̄0̄+A.B̅.C̄0̄+A.B.C0
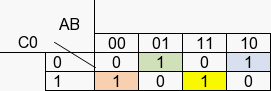
Dans cette méthode, nous rencontrons un problème, il n’est pas possible de faire des regroupements et par conséquent, d’effectuer une réduction. Nous devons utiliser une autre méthode par la réduction algébrique avec les règles de l’algèbre de Boole (ou calcul booléen).
Reprenons la forme canonique de la sortie S pour la réduire :
- Ā.B̅.C0+Ā.B-C̄0̄+A.B̅.C̄0̄+A.B.C0
Plaçons l’ensemble de la forme canonique dans des parenthèses :
- (Ā.B̅-C0+Ā.B-C̄0̄)+(A.B̅.C̄0̄+A.B.C0)
On supprime les facteurs communs dans chaque parenthèse :
- Ā.(B̅.C0+B.C̄0̄)+A.(B̅.C̄0̄+B.C0)
Pour réduire encore notre équation, on va utiliser deux règles de l’algèbre de Boole. Les symboles fonctionnels sont ⊕ pour la porte logique XOR et ⊗ pour la porte logique XNOR.
Première règle du XOR : x.ȳ+x̄.y = x⊕y
Deuxième règle du XNOR : x.y+x̄.ȳ = x⊗y = x̄⊕ȳ
Pour la première parenthèse Ā.(B̅.C0+B.C̄0̄), nous pouvons constater qu’elle est identique à la première règle XOR :
- Ā.(B̅.C0+B.C̄0̄) = x.ȳ+x̄.y = x⊕y
- = Ā.(B⊕C0)
Pour la deuxième parenthèse A.(B̅-C̄0̄+B-C0), nous pouvons utiliser la deuxième règle de XNOR :
- A.(B̅-C̄0̄+B-C0) = x.y+x̄.ȳ = x⊗y = x⊕ȳ
- = A.(B⊗C0) = A.(B̅⊕C̄0̄)
Le résultat obtenu des deux parenthèses est :
- Ā.(B⊕C0)+A.(B̅⊕C̄0̄).
On remarque dans les deux parenthèses qu’il est possible de réduire encore l’équation. Pour ce faire, nous allons poser x=B⊕C0.
Ou se trouve x.
- Ā.(B⊕C0)+A.(B̅⊕̄C̄0̄)
- = Ā.(x)+A.(x̄) soit ici la formule de XOR = A⊕x
Soit la réduction suivante pour le sortie S :
- S(A,B,C0) = A⊕B⊕C0
8. La réalisation de l’additionneur sur 1 bit
On reprend les équations précédentes.
- S(A,B,C0) = A⊕B⊕C0
- C1(A,B,C0) = A-B+A-C0+B-C0
Nous commençons par S et nous avons deux portes logiques XOR (⊕). Nous pouvons remplacer les deux portes XOR par une seule porte logique XOR fan-in 3.
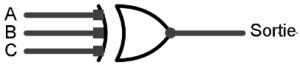
Pour la sortie C1, nous avons besoin de trois portes AND (A-B)+(A-C0)+(B-C0).
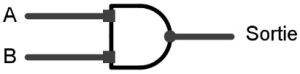


Et de deux portes OR (A-B)+(A-C0)+(B-C0) que nous allons réduire à une porte OR fan-in 3.
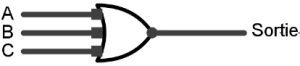
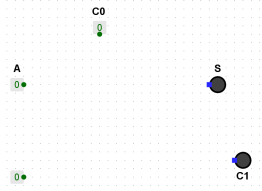
Nous disposons des éléments pour construire le logigramme. Vous pouvez utiliser le simulateur gratuit Logisim téléchargeable sur www.cburch.com/logisim/.
Première étape, nous plaçons les entrées [A,C,C0] ainsi que les deux sorties [S,C1] en utilisant des lampes.
Commençons par la fonction S=A⊕B⊕C0.
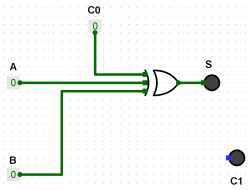
La fonction S est terminée.
Maintenant la fonction C1 (A-B)+(A-C0)+(B-C0). On commence par les portes AND (A-B)+(A-C0)+(B-C0) :
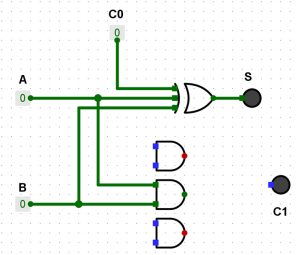
(A-B)
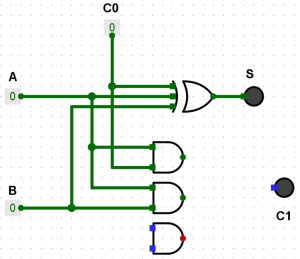
(A-C0)
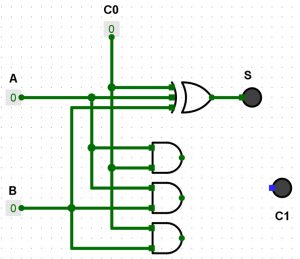
(B-C0)
Il ne nous reste plus que la porte OR (A-B)+(A-C0)+(B-C0).
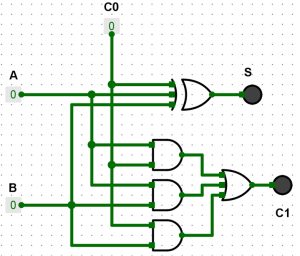
0+0=0 – [S=0]
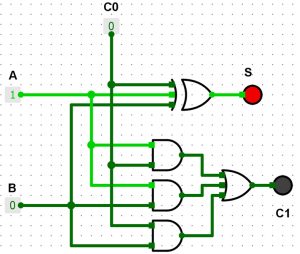
1+0=1 – [S=1]
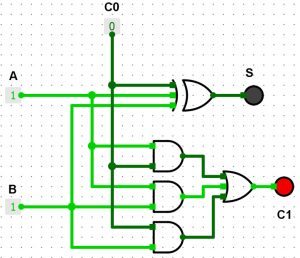
1+1=10 (2 en décimal)
C1=1 (la retenue) et S=0
L’additionneur sur 1 bit est terminé. Vous pouvez l’assembler avec le même additionneur en utilisant la sortie C1 avec C0 du prochain additionneur et ainsi de suite.
9. Annexe (liste des composants TTL)
Une liste des composants logiques, de la série 7400, utilisables pour la réalisation de circuits combinatoires est disponible sur Wikipédia.